😮 위상 정렬이란?
순서가 정해져 있는 작업을 차례로 수행해야 할 때 그 순서를 결정해주기 위해 사용하는 알고리즘입니다. 즉, 그래프의 흐름(순차적인 그래프)이 있고 다양한 조건들이 서로 얽혀있을 때, 정확히 1열로 그래프의 각 노드를 나열할 수 있도록 하는 것이 위상 정렬입니다.
예를 들어보겠습니다.

위 그림과 같이 총 3개의 과목이 있다고 가정해봅시다.
세 과목을 모두 듣기 위해서는 `자료구조 -> 알고리즘 -> 고급 알고리즘` 순서로 과목을 들어야 합니다.
만약 `자료구조 -> 고급 알고리즘 -> 알고리즘` 순서로 과목을 듣는다면, 해당 순서는 올바른 학습 순서가 아닙니다.
위상 정렬은 다음과 같은 개념이 필요합니다.

- 진입차수 : 특정한 노드가 있을 때 그 노드로 들어오는 다른 노드의 갯수를 의미합니다.
- 진출차수 : 특정한 노드가 있을 때 그 노드에서 나가는 간선의 갯수를 의미합니다.
🔎 위상 정렬 특징
1. 위상 정렬은 DAG(Directed Acyclic Graph)에만 적용이 가능합니다. 즉, 사이클이 발생하지 않는 방향 그래프이고 사이클이 발생하는 경우에는 위상정렬을 수행할 수 없습니다.
※ DAG(Directed Acyclic Graph) : 사이클이 없는 방향 그래프
2. 보통 큐로 구현하지만, 스택을 이용한 DFS를 이용해서 위상정렬을 구현할 수도 있습니다.
3. 위상 정렬은 여러 개의 답이 있을 수 있습니다. 한 단계에서 큐에 들어가는 요소가 2개 이상이라면 여러가지 답이 존재할 수 있습니다.
4. 모든 원소를 방문하기 전에 큐가 비게 된다면, 사이클이 존재한다고 판단할 수도 있습니다. 왜냐하면, 사이클에 포함된 원소 중에서 해당되는 어떠한 원소도 큐에 들어가지 못하게 되기 때문입니다. (즉, 사이클에 포함된 노드는 진입차수가 0이 되지 않아서 큐에 들어갈 수 없기 때문에 큐가 비게 된다.)
⚙️ 위상 정렬 동작과정
위상 정렬 동작과정은 스택과 큐를 이용해서 구현할 수 있습니다. 기본적으로는 큐를 이용한 방식을 선호하므로 큐를 기준으로 설명하겠습니다.
1. 진입차수가 0인 정점을 큐에 삽입합니다.
2. 큐에서 원소를 꺼내 연결된 모든 간선을 제거합니다.
3. 간선 제거 이후에 진입차수가 0이 된 정점을 큐에 삽입합니다.
4. 큐가 빌 때까지 2번과 3번 과정을 반복합니다. 모든 원소를 방문하기 전에 큐가 빈다면, 사이클이 존재하는 것이고 모든 원소를 방문했다면 큐에서 꺼낸 순서가 위상 정렬의 결과입니다.
예를 들어서 설명해보겠습니다.
📌 위상 정렬의 예시
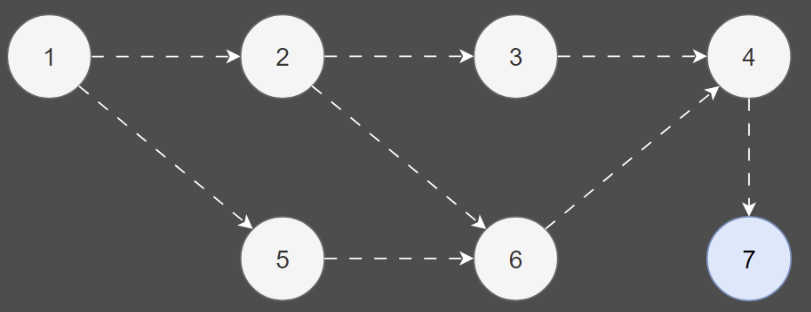
1. 진입차수가 0인 노드 1을 큐에 담습니다.

| 노드 | 1 | 2 | 3 | 4 | 5 | 6 | 7 |
| 진입차수 | 0 | 1 | 1 | 2 | 1 | 2 | 1 |
| 큐 | 노드1 |
2. 큐에 담긴 노드1을 꺼내어, 해당 노드에서 출발하는 간선을 모두 그래프에서 제거합니다. 그 후 진입차수가 0인 노드를 큐에 담습니다.

| 노드 | 1 | 2 | 3 | 4 | 5 | 6 | 7 |
| 진입차수 | 0 | 0 | 1 | 2 | 0 | 2 | 1 |
| 큐 | 노드2 | 노드5 |
3. 큐에 담긴 노드2를 꺼내어, 해당 노드에서 출발하는 간선을 모두 그래프에서 제거합니다. 그 후, 진입차수가 0인 노드를 큐에 담습니다.

| 노드 | 1 | 2 | 3 | 4 | 5 | 6 | 7 |
| 진입차수 | 0 | 0 | 0 | 2 | 0 | 2 | 1 |
| 큐 | 노드5 | 노드3 |
4. 큐에 담긴 노드 5를 꺼내어, 해당노드에서 출발하는 간선을 모두 그래프에서 제거합니다. 그 후, 진입차수가 0인 노드를 큐에 담습니다.

| 노드 | 1 | 2 | 3 | 4 | 5 | 6 | 7 |
| 진입차수 | 0 | 0 | 0 | 2 | 0 | 0 | 1 |
| 큐 | 노드3 | 노드6 |
5. 큐에 담긴 3을 꺼내어, 해당 노드에서 출발하는 모두 그래프에서 제거합니다. 그 후, 진입차수가 0인 노드가 존재하지 않으므로 넘어갑니다.

| 노드 | 1 | 2 | 3 | 4 | 5 | 6 | 7 |
| 진입차수 | 0 | 0 | 0 | 1 | 0 | 0 | 1 |
| 큐 | 노드6 |
6. 큐에 담긴 노드 6을 꺼내어, 해당 노드에서 출발하는 간선을 모두 그래프에서 제거합니다. 그 후, 진입차수가 0인 노드를 큐에 담습니다.

| 노드 | 1 | 2 | 3 | 4 | 5 | 6 | 7 |
| 진입차수 | 0 | 0 | 0 | 0 | 0 | 0 | 1 |
| 큐 | 노드4 |
7. 큐에 담긴 노드 4를 꺼내어, 해당 노드에서 출발하는 간선을 모두 그래프에서 제거합니다. 그 후, 진입차수가 0인 노드를 큐에 담습니다.
| 노드 | 1 | 2 | 3 | 4 | 5 | 6 | 7 |
| 진입차수 | 0 | 0 | 0 | 0 | 0 | 0 | 0 |
| 큐 | 노드7 |
8. 큐에 담긴 노드 7을 꺼내고 나면, 출발하는 간선과 전입차수가 0인 노드가 존재하지 않습니다. 이렇게 큐에서 꺼내어진 노드 순서대로 출력하여 위상정렬의 결과를 나타냅니다.
위상 정렬 출력 결과 : 1 → 2 → 5 → 3 → 6 → 4 → 7
👩💻 위상 정렬 코드
from collections import deque
# 노드의 개수와 간선의 개수를 입력받음
num_nodes, num_edges = map(int, input().split())
# 각 노드의 진입차수를 기록하는 리스트
in_degree = [0] * (num_nodes + 1)
# 그래프를 인접 리스트로 표현
adj_list = [[] for _ in range(num_nodes + 1)]
# 간선 정보를 입력받아 그래프와 진입차수 테이블을 생성
for _ in range(num_edges):
u, v = map(int, input().split())
adj_list[u].append(v)
in_degree[v] += 1
def topological_sort():
# 위상 정렬 결과를 저장할 리스트
sorted_order = []
# 진입차수가 0인 노드를 저장할 큐
queue = deque()
# 모든 노드를 검사하여 진입차수가 0인 노드를 큐에 추가
for node in range(1, num_nodes + 1):
if in_degree[node] == 0:
queue.append(node)
# 큐가 빌 때까지 반복
while queue:
# 큐에서 노드를 꺼내서 결과 리스트에 추가
current_node = queue.popleft()
sorted_order.append(current_node)
# 현재 노드와 연결된 모든 노드의 진입차수를 감소시키고
# 진입차수가 0이 되면 큐에 추가
for neighbor in adj_list[current_node]:
in_degree[neighbor] -= 1
if in_degree[neighbor] == 0:
queue.append(neighbor)
# 위상 정렬 결과를 출력
for node in sorted_order:
print(node, end=" ")
# 위상 정렬 함수 호출
topological_sort()
# 예시
# 7 8
# 1 2
# 1 5
# 2 3
# 2 6
# 3 4
# 4 7
# 5 6
# 6 4
'Computer Science > Algorithm' 카테고리의 다른 글
| [알고리즘/파이썬] DFS와 BFS의 개념과 구현 (0) | 2024.08.09 |
|---|

