[알고리즘/파이썬] DFS와 BFS의 개념과 구현

그래프 탐색 알고리즘

먼저 그래프 탐색 알고리즘이란,

여러 개체들이 연결되어 있는 자료구조인 그래프에서 특정 개체를 탐색하고 찾기 위한 알고리즘이다.

 

그래프 탐색 알고리즘 대표적인 유형이 DFS(깊이우선탐색)와 BFS(너비우선탐색)이다.

 

출처 : https://iq.opengenus.org/dfs-vs-bfs/#google_vignette

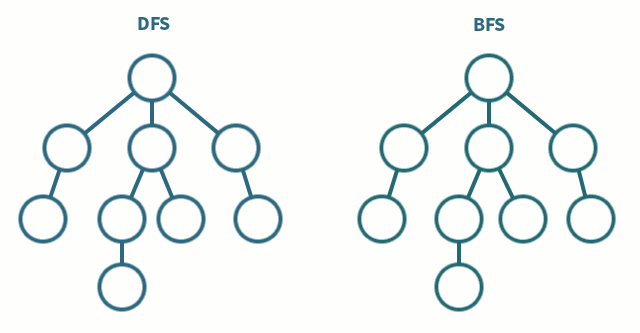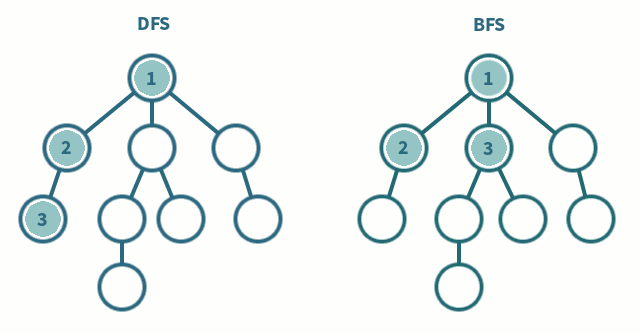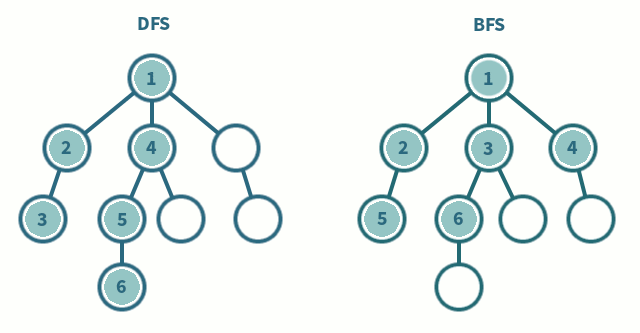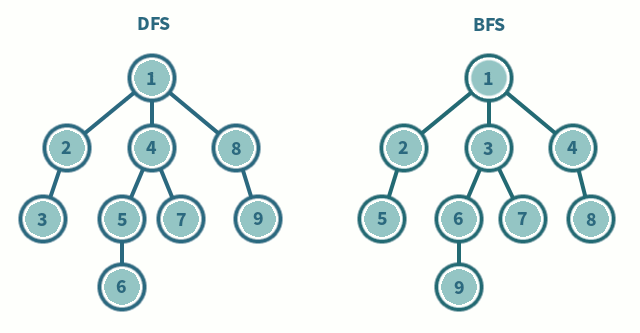
드라마 정주행을 비유해봤을 때, 한 드라마를 처음부터 끝까지 몰아봐야 하는 유형이 DFS이고, 모든 드라마 여러 개를 하나씩 본방사수하면서 챙겨봐야 하는 유형이 BFS이다.

 

대표적인 그래프 탐색 알고리즘 유형

1. 경로탐색 유형 : 최소거리 구하기, 최단 시간 구하기
2. 네트워크 유형 : 여러 개체들이 주어진 상태에서 연결되어 있는 그룹의 갯수를 구하기, 그룹 안에서 개체들이 연결되어 있는지의 여부 판단
3. 조합 유형 : 여러가지의 조합을 전부 만들고 비교해보기

 

DFS/BFS 구현 방법

우선, 파이썬으로 그래프를 입력받는 방법부터 알아보자.

파이썬에서는 보통 그래프를 딕셔너리 자료형으로 입력받는 것을 가장 선호한다.

밑의 그림과 같이 노드 간 방향이 있는 방향그래프일 경우 다음와 같이 딕셔너리 타입의 G에 저장할 수 있다.

myGraph = {
    'A': ['B', 'C', 'D'], # A번 노드와 연결된 노드들
    'B': ['A', 'E'], # B번 노드와 연결된 노드들
    'C': ['A', 'F', 'G'], # C번 노드와 연결된 노드들
    'D': ['A', 'H'], # D번 노드와 연결된 노드들
    'E': ['B', 'I'], # E번 노드와 연결된 노드들
    'F': ['C', 'J'], # F번 노드와 연결된 노드들
    'G': ['C'], # G번 노드와 연결된 노드들
    'H': ['D'], # H번 노드와 연결된 노드들
    'I': ['E'], # I번 노드와 연결된 노드들
    'J': ['F'] # J번 노드와 연결된 노드들
}

 

1. DFS 구현 방법

하나의 자식노드의 자식노드들을 끝까지 파고들어서 리프노드까지 갔다가 다시 올라가서 옆의 형제 노드들을 방문하는 것이다. 한 놈만 끝까지 패는 유형이기 때문에, 스택과 재귀함수가 가장 일반적이다.

 

ex) 덧셈만 끝까지 해보고 뺄셈을 하나씩 조합해보면서, 모든 경우의 수를 확인한다.

 

스택 자료구조를 이용할 경우

1. 탐색 시작 노드를 스택에 삽입하고 방문 처리를 한다.
2. 스택의 최상단 노드에 방문하지 않은 인접 노드가 있으면 그 인접 노드를 스택에 넣고 방문 처리를 한다. 방문하지 않은 인접 노드가 없으면 스택에서 최상단 노드를 꺼낸다.
3. 2번의 과정을 더 이상 수행할 수 없을 때까지 반복한다.

여기서, 방문 처리는 스택에 한 번 삽입되어 처리된 노드가 다시 삽입되지 않게 체크하는 것을 말한다. 이렇게 방문 처리를 함으로써 각 노드를 한 번씩만 처리할 수 있다.

myGraph={
    'A':['B','C','D'],    # A번 노드와 연결된 노드들
    'B': ['A', 'E'],      # B번 노드와 연결된 노드들
    'C': ['A', 'F', 'G'], # C번 노드와 연결된 노드들
    'D': ['A', 'H'],      # D번 노드와 연결된 노드들
    'E': ['B', 'I'],      # E번 노드와 연결된 노드들
    'F': ['C', 'J'],      # F번 노드와 연결된 노드들
    'G': ['C'],           # G번 노드와 연결된 노드들
    'H': ['D'],           # H번 노드와 연결된 노드들
    'I': ['E'],           # I번 노드와 연결된 노드들
    'J': ['F']            # J번 노드와 연결된 노드들
}


# 스택을 이용했을 때
def dfs(graph,start_node):
    global visited
    # 방문한 노드를 담을 배열
    visited=list()
    # 정점과 인접한 노드, 즉 방문 예정인 노드를 담을 배열
    stack=list()

    # 시작노드를 stack에 넣어주고 시작함
    stack.append(start_node)

    # 더이상 방문할 노드가 없을 때까지 반복함
    while stack:
        # 방문할 노드를 앞에서부터 하나씩 꺼내기
        node=stack.pop()
        
        # 방문한 노드가 아니라면
        if node not in visited:
            # visited 배열에 추가
            visited.append(node)
            # 스택에 거꾸로 넣어주기 (탐색 순서를 정확히 유지하기 위해)
            stack.extend(reversed(graph[node]))

    return visited

dfs(myGraph,'A')
print(visited)

# 정답 : ['A', 'B', 'E', 'I', 'C', 'F', 'J', 'G', 'D', 'H’]

 

재귀함수로 구현할 경우, 재귀함수를 타고 가서 탈출 조건에 먼저 도달하고 그 다음 파라미터를 하나씩 바꿔가면서 정답을 찾으면 된다.

# 재귀 기반 DFS 함수
def dfs_recursive(graph, node, visited):
    # 현재 노드를 방문 처리하고 출력
    visited.append(node)

    # 인접한 모든 노드를 방문
    for neighbor in graph[node]:
        if neighbor not in visited:
            dfs_recursive(graph, neighbor, visited)

# 그래프 정의
myGraph = {
    'A': ['B', 'C', 'D'],
    'B': ['A', 'E'],
    'C': ['A', 'F', 'G'],
    'D': ['A', 'H'],
    'E': ['B', 'I'],
    'F': ['C', 'J'],
    'G': ['C'],
    'H': ['D'],
    'I': ['E'],
    'J': ['F']
}

# 방문한 노드를 기록할 리스트
visited = []

# DFS 시작
dfs_recursive(myGraph, 'A', visited)

print(visited)

 

2. BFS 구현 방법

하나의 자식노드를 먼저 방문하고 그 다음 같은 형제노드들을 방문하는 것, 즉 레벨 단위로 검색을 하는 것이다. 쉽게 말하자면, 가까운 노드부터 탐색하는 알고리즘이다.

 

먼저 큐에 노드를 넣고, 턴을 돌면서 가장 오래된 노드를 꺼내 연결된 노드를 다시 큐에 추가한다. 이 과정을 큐가 빌 때까지 반복하면서 가장 먼저 넣었던 것을 꺼내는 식으로 모든 노드를 탐색한다.

 

→ 순서가 보장되어야 되기 때문에 Queue나 LinkedList를 사용하는 것이 좋다!

 

큐 자료구조를 이용할 경우

1. 탐색 시작 노드를 큐에 삽입하고 방문 처리를 한다.
2. 큐에서 노드를 꺼내 해당 노드의 인접 노드 중에서 방문하지 않은 노드를 모두 큐에 삽입하고 방문 처리를 한다.
3. 2번의 과정을 더 이상 수행할 수 없을때 까지 반복한다.

→ 즉, 노드를 방문하면서 인접한 노드 중 방문하지 않았던 노드의 정보만 큐에 넣어 먼저 큐에 들어있던 노드부터 방문하면 된다.

# 그래프 정의
myGraph = {
    'A': ['B', 'C', 'D'],
    'B': ['A', 'E'],
    'C': ['A', 'F', 'G'],
    'D': ['A', 'H'],
    'E': ['B', 'I'],
    'F': ['C', 'J'],
    'G': ['C'],
    'H': ['D'],
    'I': ['E'],
    'J': ['F']
}

# 큐를 이용했을 때
def bfs(graph,start_node):
    global visited
    # 방문한 노드들을 담을 배열
    visited=list()
    # 정점과 인접한 노드, 즉 방문 예정인 노드를 담을 배열
    queue=list()

    # 시작노드를 queue에 넣어주고 시작함
    queue.append(start_node)

    # 더이상 방문할 노드가 없을 때까지 반복하기
    while queue:
        # 방문할 노드를 앞에서부터 하나씩 꺼내기
        node=queue.pop(0)

        # 방문한 노드가 아니라면
        if node not in visited:
            # 방문한 배열에 추가
            visited.append(node)
            # 해당노드의 자식 노드로 추가
            queue.extend(graph[node])

    return visited

bfs(myGraph,'A')

print(visited)