[자료구조] 힙(Heap)과 우선순위 큐(Priority Queue)

힙은 우선순위 큐를 구현하기 위해서 사용되는 자료구조입니다.

우선순위 큐란?

우선순위가 가장 높은 데이터를 가장 먼저 추출하는 자료구조입니다. 데이터를 우선순위에 따라 처리하고 싶을 때 사용합니다.

예를 들어, 물건 데이터를 자료구조에 넣었다가 가치가 높은 물건부터 꺼내서 확인해야 되는 경우에 사용됩니다.

자료구조	추출되는 데이터 결과
스택	가장 나중에 삽입된 데이터
큐	가장 먼저 삽입된 데이터
우선순위 큐	가장 우선순위가 높은 데이터

우선순위 큐를 구현하는 방법

1. 단순히 리스트를 이용하여 구현합니다.

→ 차례대로 연달아 넣고, 리스트에서 데이터를 꺼낼 때 값들을 확인하고 가장 값이 큰 데이터부터 뽑아서 추출합니다.

2. 힙을 구현하여 구현합니다.

데이터의 갯수가 N개라고 가정하고 구현 방식에 따라서 시간복잡도를 비교하였을 때의 결과는 아래와 같습니다.

우선순위 큐 구현방식	삽입 시간	삭제 시간
리스트	O(1)	O(N)
힙(Heap)	O(logN)	O(logN)

여기서, 우선순위 큐에서 단순히 N개의 데이터를 힙에 넣었다가 모두 꺼내는 작업은 정렬과 동일합니다.

→ 그 자체로써 정렬이 수행된다는 점이 특징입니다.

힙(Heap)이란?

우선순위 큐를 위하여 만들어진 자료구조입니다. 여러 개의 값들 중에서 최댓값이나 최솟값을 빠르게 찾아내도록 하는 자료구조입니다. 간단하게 말하자면, 부모 노드의 키 값이 자식 노드의 키 값보다 항상 큰(작은) 이진 트리를 말합니다.

→ 보통 최댓값, 최솟값을 찾는 연산을 빠르게 하기 위해서는 고안된 완전 이진트리를 기본으로 합니다.

힙(Heap)의 특징

1. 힙은 완전 이진 트리 자료구조의 일종입니다.

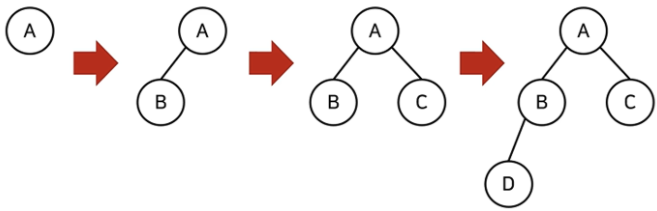
→ 이때 완전 이진 트리란, 루트 노드부터 시작하여 왼쪽 자식노드, 오른쪽 자식 노드 순서대로 데이터가 차례대로 삽입되는 트리를 의미합니다. 마지막 레벨을 제외하고 모든 레벨이 완전히 채워져 있으며, 마지막 레벨의 모든 노드는 가능한 한 가장 왼쪽에 있습니다.

2. 항상 루트 노드가 최댓값 또는 최솟값을 가지며, 이를 O(1) 시간 내에 접근할 수 있습니다. 삽입과 삭제의 시간 복잡도는 O(log n)으로 매우 효율적입니다.

3. 최소 힙(min heap)

루트 노드가 가장 작은 값을 가집니다.
따라서 값이 작은 데이터가 우선적으로 제거됩니다.

4. 최대 힙(max heap)

루트 노드가 가장 큰 값을 가집니다.
따라서 값이 큰 데이터가 우선적으로 제거됩니다.

5. 힙 트리에서는 중복된 값을 허용합니다. (이진 트리에서는 중복된 값을 허용하지 않습니다.)

힙(Heap)의 종류

1. 최소 힙 구성 함수 : Min-Heapify()

하나의 데이터가 들어왔을 때, 들어온 데이터로부터 부모 노드로 상향식으로 거슬러 올라가면서 매번 부모보다 자신의 값이 더 작은 경우에 위치를 교체할 수 있도록 합니다.

예를 들어, 새로운 데이터인 4가 들어왔을 때 최소 힙 성질을 만족하지 않으므로 교체하면서 최소 힙 함수를 구성할 수 있도록 합니다.

👀 여기서 최소 힙 Min-Heapify() 의 시간복잡도는?

기본적으로, 힙은 완전 이진트리 구조를 따르기 때문에 균형잡힌 트리로써 동작을 합니다. 그러므로, 항상 부모 쪽으로 거슬러 올라가거나 다시 내려올 때 최악의 경우에도 O(logN)의 시간 복잡도를 유지할 수 있습니다.

2. 최대 힙 구성 함수 : Max-Heapify()

하나의 데이터가 들어왔을 때, 들어온 데이터로부터 부모 노드로 상향식으로 거슬러 올라가면서 매번 부모노드보다 자신의 값이 더 큰 경우에 위치를 교체할 수 있도록 합니다.

힙(Heap)의 적용

힙에서 원소가 삽입될 때

힙에 새로운 요소가 들어오면, 일단 새로운 노드를 힙의 마지막 노드에 이어서 삽입합니다. 새로운 노드를 부모 노드들과 교환해서 힙의 성질을 만족시킵니다.

힙에서 원소가 삭제될 때

최대 힙에서 최댓값은 루트노드이므로 루트노드가 삭제됩니다. 삭제된 루트 노드에는 힙의 마지막 노드를 가져옵니다.

파이썬에서의 힙(Heap) 자료구조

파이썬 heapq 내장 모듈은 heapq 알고리즘을 제공합니다.

모든 부모 노드는 그의 자식 노드보다 값이 작거나 큰 이진트리 구조인데, 내부적으로는 인덱스 0에서 시작해 k번째 원소가 항상 자식 원소들(2k+1, 2k+2) 보다 작거나 같은 최소 힙의 형태로 정렬됩니다.

heapq는 내장 모듈로 별도의 설치 작업 없이 바로 사용할 수 있습니다.

힙(Heap) 생성 & 원소 추가

heapq 모듈은 리스트를 최소 힙처럼 다룰 수 있기 하기 때문에, 빈 리스트를 생성한 후 heapq의 함수를 호출할 때마다 리스트를 인자에 넘깁니다.

아래 예시를 통해서 설명하겠습니다.

1. heappush (원소 추가)

heappush 함수를 통해 item을 heap에 추가합니다.

호출 형태 : heapq.heappush(heap,item)

import heapq

heap=[]
heapq.heappush(heap,100)
heapq.heappush(heap,1)
heapq.heappush(heap,50)
heapq.heappush(heap,70)

print(heap)

→ 리스트를 최소 힙처럼 다룰 수 있도록 하기 때문에 heapq 함수를 호출할 때마다 리스트를 인자에 넘깁니다.

정확한 이해를 위해서 예를 통해 설명하겠습니다.

1. 4을 추가: 현재 힙은 [4]입니다.

트리 구조:

2. 1을 추가: 1이 4보다 작으므로 루트로 올라가고, 4는 1의 자식 노드로 이동합니다. 이때 힙은 [1, 4]가 됩니다.

트리 구조:

1
/
4

3. 3을 추가: 3은 4보다 작고, 1보다는 크므로 1의 자식 노드로 추가됩니다. 이때 힙은 [1, 4, 3]이 됩니다.

트리 구조:

  1
 / \
4   3

4. 7을 추가: 7은 모든 기존 노드보다 크기 때문에 마지막에 추가되며, 트리 구조에서 왼쪽 자식 노드로 추가됩니다. 이때 힙은 [1, 4, 3, 7]이 됩니다.

2. heappop (원소 삭제)

heappop는 가장 작은 원소를 힙에서 제거함과 동시에 그를 결괏값으로 리턴합니다. 비어 있는 경우 IndexError가 호출됩니다.

호출 형태 : heapq.heappop(item)

result=heapq.heappop(heap)

print(result)
print(heap)

3. 힙 생성(변환)

heapify 함수를 통해 list를 heap으로 변환합니다.

호출 형태 : heapify(list)

import heapq

heap1=[70,30,100]
heapq.heapify(heap1)

print(heap1)

이처럼 파이썬에서는 기본적으로 min heap으로 구성되어있어서, 결과가 자연스럽게 오름차순으로 구성되는 것을 알 수 있습니다.

그러면 max heap(최대 힙)은 어떻게 구현해야 할까요?

최대 힙(Heap) 구현

이때 사용되는 개념은 아래와 같습니다.

💡 IDEA: y = -x 변환을 하면 최솟값 정렬이 최댓값 정렬로 바뀐다.

힙에 원소를 추가할 때 (-item, item)의 튜플 형태로 넣어주게 되면 튜플의 첫 번째 원소를 우선순위로 힙을 구성하게 됩니다. 이때 원소 값의 부호를 바꿨기 때문에, 최소 힙으로 구현된 heapq 모듈을 최대 힙 구현으로 바뀌게 되는 것입니다.

아래의 예시를 통해서 살펴보겠습니다.

import heapq

items = [1,3,5,7,9]

max_heap = []
for item in items:
  heapq.heappush(max_heap, (-item, item))

for i in range(len(max_heap)):
  print(max_heap[i][1],end=" ")

heappush 함수를 통해 item을 힙에 push 할 때 (-item, item)의 튜플의 형태로 넣은 것을 확인할 수 있습니다.

쉽게 말하자면, 최소 힙의 결과를 음수 형태로 변환하여서 최대 힙 형태로 출력하도록 하였기 때문에 실제로는 -item이 힙의 정렬 기준이 됩니다.

참고 자료

https://www.youtube.com/watch?v=AjFlp951nz0